Laboratory Design Project III - A Voltage Controlled Oscillator
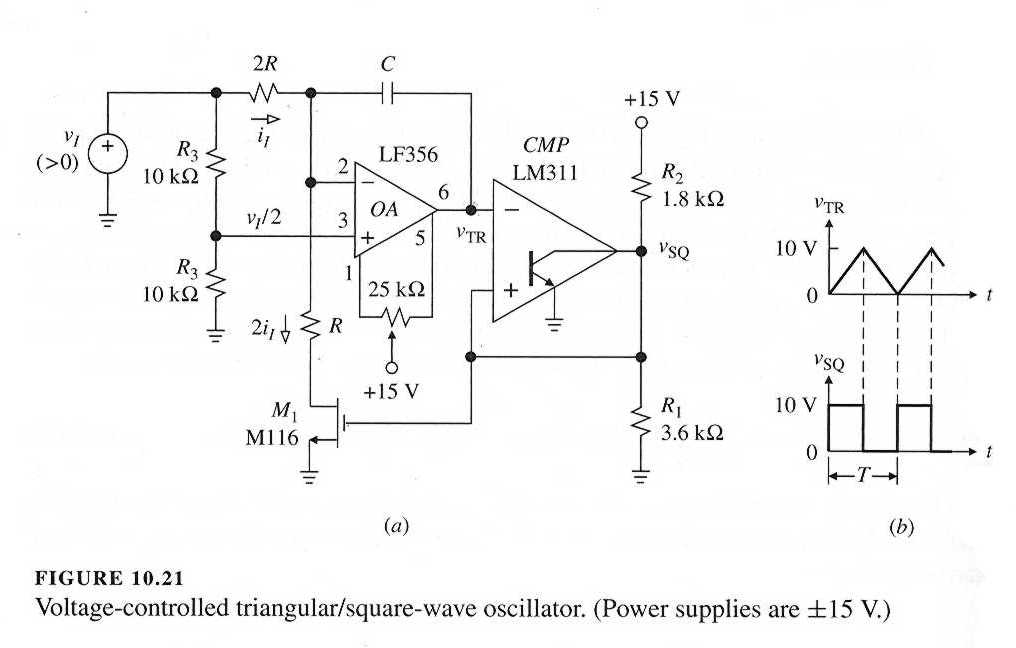
This is the third and last experiment on waveform generator circuits. It involves the voltage controlled triangular/square-wave generator circuit described in the text. The circuit is covered in section 10.4 and is given in Figure 10.21.
For all circuits, you should have 100 μF decoupling capacitors from each power supply rail to circuit ground. You should be aware that these capacitors are polar electrolytics which can explode if they are put in with the wrong polarity.
Op amps can oscillate when equipment such as an oscilloscope is connected to a circuit. This is caused by the capacitance of the connecting leads. To minimize these problems, clip a 100 Ω resistor in series with the signal lead to the oscilloscope. Use the other end of the resistor to connect to the proto board.
The 741 op amp has a fairly low slew rate and is not an appropriate op amp for this experiment. You should use one of the BiFET op amps such as the TL071, TL081, LF351, etc. These have a slew rate that is a little more than 10 times that of the 741.
Procedure
- Assemble the circuit in Fig. 10.21 omitting the 25 kΩ potentiomenter. This can be added later. For the op amp, use a TL071 or an LF351. It should be connected to the dual power supply set initially for zero volts. The LM311 comparator should be connected between the positive rail and ground. Instead of the MOSFET, use a 2N4401 NPN BJT. The BJT must have a resistor in series with its base to limit the base current when the BJT saturates. A suggested value for this resistor is 10 kΩ. If it is found that the BJT does not saturate, the resistor value must be decreased. The example in the text uses a 1.25 nF capacitor for C. This can be replaced with a value of 1 nF. With R2 equal to the value used in the text, use the equation derived in class to calculate R1 to obtain a positive peak voltage of the triangular waveform of VTRp = 10 V. Assume VBE = 0.65 V for the BJT and V+ = 15 V for the positive power supply voltage.
- Connect the channel 1 input to the oscilloscope to the triangle wave output vTR and the channel 2 input to the square-wave output vSQ. Set the oscilloscope coupling to dc.
- Set the function generator to its low output impedance mode. Connect its output to the circuit input. Adjust the function generator output for a dc offset of +5 V and an ac voltage of 0 V.
- Adjust the power supply voltages for +15 V and -15 V outputs. You should observe triangular and square-wave waveforms on the oscilloscope. Verify that VTRp = 10 V. If you do not obtain 10 V, check your calculation for R2. Change the resistor to the 5% value that gives the closest peak value of 10 V.
- The lowest or minimum value of the triangle wave should be close to 0 V. If it is not, add a 10 kΩ offset adjust potentiometer to the op amp. The connection of this potentiometer differs with op amps, so check the specification sheet for your op amp to determine the correct pins for this connection. You should be able to set the potentiometer to obtain a lower value of 0 V.
- Measure the frequency of oscillation. It should agree with the equation derived in class. If it is within 10%, your circuit is operating correctly.
- The next step is to measure the linearity of the frequency control.
- Change the dc offset of the function generator to 0.1 V. Measure the frequency. Increase the dc offset to 1 V. Measure the frequency. Increase the dc offset in steps of 1 V to 10 V and measure the frequency for each value. This will give a total number of 11 data points. If the function generator does not want to cooperate in setting the dc voltages, use a potentiometer connected between +15 V and ground to replace the function generator and set the voltages. To isolate the output resistance of the potentiometer from the circuit, connect an op amp as a unity gain buffer between the potentiometer wiper and the circuit input.
- In your report, use a least-squares regression analysis to obtain the equation for the best straight line that fits the data. Plot the data and the equation on the same graph to verify that the measured data comes close to the straight-line curve fit. How close does the equation come to the theoretical equation?
- The next step is to measure the frequency spectra of the output signals.
- With the oscilloscope set for ac coupling and the oscillator frequency set for 5 kHz, use the FFT facility of the oscilloscope to observe and record the spectra of the two output signals. You should observe only odd harmonics of the fundamental. If even harmonics are present, the duty cycle of the square wave is not 50%. If even order harmonics are present, you can neglect them if they appear to be small compared to the fundamental. Note that the triangular wave has much smaller harmonics than the square wave. This can easily be predicted by a theoretical Fourier transform analysis of the two waveforms.
- Adjust the function generator to put out an ac voltage with a frequency of 100 Hz on top of the dc offset voltage used above. Adjust the amplitude of the ac voltage and observe its effect of modulating the frequency of the output waveforms. Change the frequency of the ac voltage to observe how the frequency modulation responds.
- With the oscilloscope set to ac coupling, use its FFT facility to observe how the spectra of the signals change when the frequency is modulated. Determine and record several combinations of ac input voltage and frequency that produce spectra where the sidebands of the harmonics look interesting and do not overlap. No more than 4 combinations need to be identified. Note how the widths of the sidebands vary with the amplitude and frequency of the ac modulating voltage.
- Use the spectrum analyzer in the Low Noise Electronics Laboratory to measure the spectra of the output signals for the combinations of ac modulating voltage and frequency identified above. The spectrum analyzer must be set for ac coupling at its input to block the dc output from the circuit. Record the spectra.

